07 查找
常用搜索算法详解
1. 顺序(线性)搜索
顺序搜索是一种简单直观的搜索算法,它按顺序逐个检查数组中的元素,直到找到目标元素或遍历整个数组。其时间复杂度为O(n),适用于小型数据集。
1 | def sequential_search(arr, target): |
1 | /** |
2. 二分(折半)搜索
[!Note]
前提是有序
二分搜索是一种高效的搜索算法,要求数组必须是有序的。它通过不断将目标值与数组中间元素比较,将搜索范围缩小一半,直到找到目标或范围缩小到空集。其时间复杂度为O(log n)。
2.1 二分(折半)搜索思路分析
- 首先确定该数组的中见下标 mid = (left + right)/2
- 让需要查找的数findVal与arr[mid]比较
2.1 findVal > arr[mid] , 说明你要查找的数在mid 的右边, 因此需要递归的向右查找
2.2 findVal < arr[mid], 说明你要查找的数在mid 的左边, 因此需要递归的向左查找
2.3 findVal == arr[mid] 说明找到,就返回
[!TIP] 递归退出的条件:找到就返回;递归完数组仍然未找到,left>right
2.2 代码实现二分(折半)搜索
1 | def binary_search(arr, target): |
1 | public static int binarySearch(int[] arr, int left, int right, int value) { |
1 | package org.example; |
3. 插值搜索
3.1 插值搜索介绍
插值搜索是一种改进的二分搜索算法,特别适用于数据分布均匀的有序数组。它通过目标值在数组中的大致位置估计,从而更快地缩小搜索范围。插值搜索的时间复杂度与二分搜索类似,也是O(log n)。
[!TIP] 思路:插值搜索的核心原理是根据目标值在数组中的估计位置,通过插值公式动态调整搜索范围。它假设数据分布较均匀,因此在估计目标位置时更为准确。
3.2 插值搜索步骤
- 初始化搜索范围的低位(low)和高位(high)。
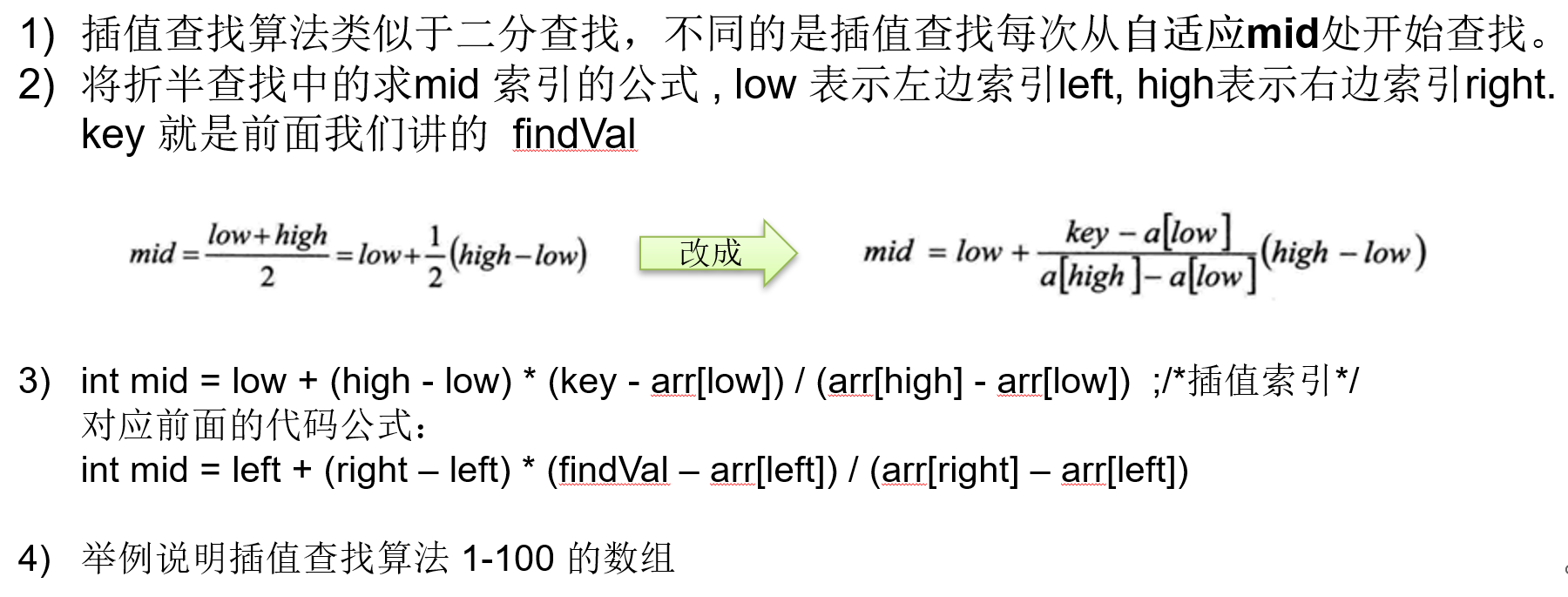
- 计算当前猜测值(mid)使用插值公式:
mid = low + (target - arr[low]) * (high - low) // (arr[high] - arr[low])。 - 比较arr[mid]与目标值的大小关系。
- 根据比较结果更新搜索范围。
- 重复以上步骤直到找到目标值或搜索范围为空。
3.3 代码实现插值搜索
1 | def interpolation_search(arr, target): |
1 | package org.example; |
4. 斐波那契搜索
4.1 介绍
斐波那契搜索是一种对有序数组进行搜索的算法,结合了二分搜索和黄金分割的思想。它通过斐波那契数列来确定分割点,从而减少比较次数。其时间复杂度为O(log n)。
4. 2 斐波那契搜索原理
[!Note] 斐波那契搜索的核心原理是通过计算斐波那契数列中的数值,找到大于等于数组长度的最小斐波那契数。然后利用斐波那契数列中的两个相邻值及一个偏移量,在数组中确定分割点,从而缩小搜索范围。
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid不再是中间或插值得到,而是位于黄金分割点附近,mid=low+F(k-1)-1(F代表斐波那契数列),如下图所示
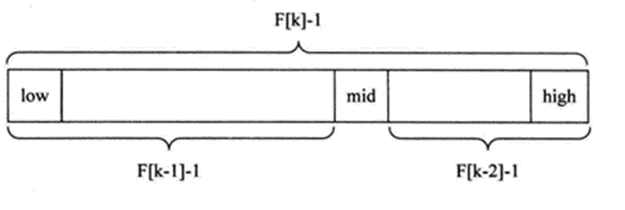
对F(k-1)-1的理解:
1)由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质,可以得到 (F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 。该式说明:只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段,即如上图所示。从而中间位置为mid=low+F(k-1)-1
2)类似的,每一子段也可以用相同的方式分割
3)但顺序表长度n不一定刚好等于F[k]-1,所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只要能使得F[k]-1恰好大于或等于n即可,由以下代码得到,顺序表长度增加后,新增的位置(从n+1到F[k]-1位置),都赋为n位置的值即可。
4. 3 斐波那契搜索步骤
- 计算斐波那契数列,找到大于等于数组长度的最小斐波那契数。
- 初始化斐波那契数列的两个相邻值及一个偏移量。
- 在数组中确定分割点,根据比较结果更新搜索范围。
- 重复以上步骤直到找到目标值或搜索范围为空。
4. 4 代码实现斐波那契搜索
1 | def fibonacci_search(arr, target): |
1 | package org.example; |
- 标题: 07 查找
- 作者: moye
- 创建于 : 2024-07-22 17:18:02
- 更新于 : 2025-12-12 18:22:53
- 链接: https://www.kanes.top/2024/07/22/07 查找/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。